Molecular Dynamics Simulation of Hard Spheres — Priority Queue In Action With Java

Event Driven Simulation (Since This Platform Only Supports GIF so Some Frames are skipped and simulation is not smooth as expected)

Hey! there , I am back again with an interesting Data Structure And Algorithm problem namely Event Driven Simulation. You might wonder why my recent articles are based on simulations. If not check my previous articles on Monte Carlo Simulation : Estimate Percolation Threshold In Java, Conway’s Game Of Life: A Cellular Automaton and The Art Of Computer And Mathematics: Barnsley Fern. It has intrigued me that how invention of efficient data structures and algorithms has made is possible to simulate real world scenario on computers. Same applies for Event Driven Simulation.

You might question why is it necessary to simulate anything that already exists in the natural world, why can’t we just observe its characteristics in the natural world. The idea is that we wanna study some sort of property of the natural world without creating any effects to other existing entities(A rough definition perhaps).

Event Driven Simulation is not just limited to computer science , perhaps it dates back to Einstein studying motion of pollen grains. So, the GIF you see above can be taken as representation of some sort of particles with some mass that behaves according to the laws of elastic collision. This simulation is only possible due to existence of priority queues. If not then it would have taken quadratic time to compute each collisions. And if you are new or a veteran in the field of computer science ,you might know that Quadratic time is a big NO.

The main goal of this simulation is to show the motion of N moving particles that behaves according to the laws of elastic collision. This problem is modeled as Hard disc model in computer science where each moving particle interacts via elastic collision with other particles and are bounded by walls. Every particle is a disc that has its own properties like velocity , position , mass, radius or some other forces like kinetic energy , gravity or friction. In this article, We will be only seeing properties like velocity , position , mass and radius.

Lets Get Technical

As usual all the codes can be found at my private GitHub repository Event Driven Simulation

Let’s break down the simulation into tiny little problems, this way we can tackle smaller problem leading to solution of a bigger problem.

1. Firstly and foremost we need a class that presents the characteristic of a particle that moves freely in a closed environment. We will be referring this as a Particle Problem.
2. Next we need to detect if there are any collision happening . This is where Priority Queue shines. We beforehand predict the possible collision between particles and only calculate the effect of collision between two particle when the event occurs. We will call it as Event Problem.
3. And finally we need a class that incorporates Particles and Events so that it creates a suitable environment for simulation. We will call it as Collision System Problem.

Particle Problem’s Solution

To solve this issue we need a class that can represent the properties of a particle. This class will requires properties like x, y coordinates to present particle on a 2D plane. It’s x and y velocities , particle’s radius , mass and other fancy attributes. This class should also incorporate behaviors like drawing , calculating time to hit horizontal or vertical axes and time required to collide with a given particle and many more . Much on that later.

So I created a class namely Particle with the following properties

private double rx, ry;
private double vx, vy;
private final double radius;
private final double mass;
private int count;
int r, g, b;

Here rx and ry represents the x and y coordinates whereas vx and vy represent x and y velocities. Similarly radius , mass , count (counting how many times a particular particle made collision with other particle) and r,g,b for its color.

public Particle() {
    radius = 0.01;
    mass = 0.5;
    rx = StdRandom.uniform(0.0, 1.0);
    ry = StdRandom.uniform(0.0, 1.0);
    vx = StdRandom.uniform(-0.005, 0.005);
    vy = StdRandom.uniform(-0.005, 0.005);
    r = StdRandom.uniform(0, 255);
    g = StdRandom.uniform(0, 255);
    b = StdRandom.uniform(0, 255);
}

Nothing fancy here just initializing the variables with some random values.

public void move(double dt) {
    rx += vx * dt;
    ry += vy * dt;
}

Since the particle moves freely , the move function mimics the motion of the particle . Here new coordinates are calculated using simple logic i.e velocity * time.

public void draw() {
    StdDraw.setPenColor(new Color(r, g, b));
    StdDraw.filledCircle(rx, ry, radius);
}

Again nothing fancy , just a function to show the particle on a 2D plane.

public double timeToHitHorizontalWall() {
    if (vy > 0) return (1.0 - ry - radius) / vy;
    else if (vy < 0) return (radius - ry) / vy;
    else return Double.POSITIVE_INFINITY;
}
public double timeToHitVerticalWall() {
    if (vx > 0) return (1.0 - rx - radius) / vx;
    else if (vx < 0) return (radius - rx) / vx;
    else return Double.POSITIVE_INFINITY;
}

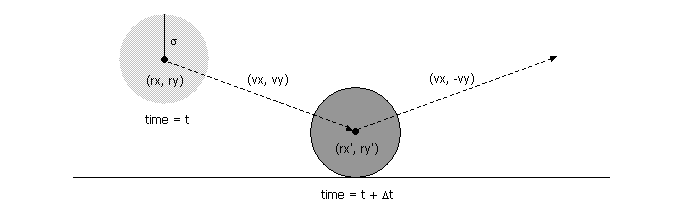
A tad bit of high school physics is required. As we know velocity is the rate of change of its position with respect to time. So time taken for an object to reach certain distance i.e distance over velocity. Same is applied in the above mentioned function.

public void bounceOffVerticalWall() {
    vx = -vx;
    count++;
}

public void bounceOffHorizontalWall() {
    vy = -vy;
    count++;
}

These two function just sets its axis to negative whenever they touch vertical or horizontal walls respectively.

public double timeToHit(Particle that) {
    if (this == that) return Double.POSITIVE_INFINITY;
    double dx = that.rx - this.rx;
    double dy = that.ry - this.ry;
    double dvx = that.vx - this.vx;
    double dvy = that.vy - this.vy;
    double dvdr = dx * dvx + dy * dvy;
    if (dvdr > 0) return Double.POSITIVE_INFINITY;
    double dvdv = dvx * dvx + dvy * dvy;
    if (dvdv == 0) return Double.POSITIVE_INFINITY;
    double drdr = dx * dx + dy * dy;
    double sigma = this.radius + that.radius;
    double d = (dvdr * dvdr) - dvdv * (drdr - sigma * sigma);
    if (d < 0) return Double.POSITIVE_INFINITY;
    return -(dvdr + Math.sqrt(d)) / dvdv;
}

Here comes the heavy lifting. This function calculates the time taken to collide with a given particle. The mathematical analogy can be found at Princeton’s java assignment page.

As newtons second law of motion states that the acceleration of an object depends on the mass of the object and the amount of force applied to it. So, when two object collide there are some resultant of that action but here in this simulation only the change in velocity and direction are visible but more can be added onto this algorithm. There are no different logic in the above mentioned code they are just mathematical formulas to calculate the time taken for a collision to occur.

public void bounceOff(Particle that) {
    double dx = that.rx - this.rx;
    double dy = that.ry - this.ry;
    double dvx = that.vx - this.vx;
    double dvy = that.vy - this.vy;
    double dvdr = dx * dvx + dy * dvy;
    double dist = this.radius + that.radius;
    double J = 2 * this.mass * that.mass * dvdr / ((this.mass + that.mass) * dist);
    double Jx = J * dx / dist;
    double Jy = J * dy / dist;
    this.vx += Jx / this.mass;
    this.vy += Jy / this.mass;
    that.vx -= Jx / that.mass;
    that.vy -= Jy / that.mass;
    this.count++;
    that.count++;
}

After, we have done predicting the collision with a given object . Now, all we need to do is calculate the resultant of the collision. Since, no particle exhibits the same property after a collision so the respective properties must be updated. These update process is carried out using some formulas shown below.

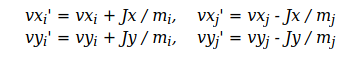
Event Problem’s Solution

The main motivation behind creating Event class is to check if the two particle collides relative to time differences. So to tackle this problem we will have to take help of java’s Comparable interface, which allows us to implement compareTo method to calculate the difference in time which we can use in future to arrange nodes or events in priority queue. As we know priority queue can be of either of max type or min type. Meaning when we delete an item within ordered priority queue it removes the maximum or minimum node relative to the type we use. So, the main motivation is to delete minimum node or node representing present time step so that events that occurs in future are examined and operated later. Hence, saving a lot of computation.

Now, we need a class that implements Comparable interface. Then, we define what should be the metric to order the Event class within the queue in compareTo method. If you are not familiar with comparable interface I suggest you to give a quick look onto that. Moreover, a event class must contain two particles : its current time step and the number of collision met by each particles.

The reason behind maintaining the number of collision is that we predict the potential collision before hand .If the particle collides with another particle before reaching the predicted time step then this event is considered as invalid .The reason for that is the particle it needed to collide with has already made a collision with another particle and has changed its velocity and direction.

public Event(double t, Particle a, Particle b) {
    time = t;
    this.a = a;
    this.b = b;
    if (a != null) countA = a.count();
    else countA = -1;
    if (b != null) countB = b.count();
    else countB = -1;
}

Initially, we maintain a collision count in two different variables and later on we compare if the event is valid or invalid.

public boolean isValid() {
    if (a != null && a.count() != countA) return false;
    if (b != null && b.count() != countB) return false;
    return true;
}

So, for an event to be valid both given particles A and B must not have made any collision with other particles. To validate the event we compare its collision count when it was initialized with the number of collision count when the event is being deleted from the queue. So, if they match then the object has not met any collision otherwise the event is invalidated and moved on to next event. We will see this process when we solve Collision System Problem.

Collision System’s Solution

This is the part where Particles and Events get tied up. As I mentioned earlier we will be using Min Priority Queue to maintain a sequence of events, and there are arrays of particles that will be randomly assigned.

The motivation behind the creation of collision system can be defined as follows:

1. Delete the impending event from the priority queue.
2. Check if the event has been invalidated (if any of the particle has made a collision before)
3. Move every other particles to time t on straight trajectory.
4. Update the velocity of the colliding particle if it meets the validation criteria.
5. Predict future particles wall and particle-particle collision and insert them onto the priority queue.

If we follow the above mentioned condition then we will have a Molecular Dynamics Simulation of Hard Spheres.

private static final double refresh = 0.2;
private MinPQ<Event> pq;
private double t = 0.0;
private Particle[] particles;

Here, refresh is just a fancy variable you can discard it if you wish to.

public CollisionSystem(Particle[] particles) {
    this.particles = particles.clone();
}

We just clone the previously initialized particles just to save few lines.

private void predict(Particle a, double limit) {
    if (a == null) return;
    for (int i = 0; i < particles.length; i++) {
        double dt = a.timeToHit(particles[i]);
        if (t + dt <= limit) {
            pq.insert(new Event(t + dt, a, particles[i]));
        }
    }
    double dtX = a.timeToHitVerticalWall();
    double dtY = a.timeToHitHorizontalWall();
    if (t + dtX <= limit) pq.insert(new Event(t + dtX, a, null));
    if (t + dtY <= limit) pq.insert(new Event(t + dtY, null, a));
}

Here, the predict method iterates over all the particles and inserts an Event with respect to the possibility of hitting another particle. Here I have used a limiting parameter namely limit which can be discarded. It is present here just to limit the simulation into arbitrary steps.

private void redraw(double limit) {
    StdDraw.clear();
    for (int i = 0; i < particles.length; i++) {
        particles[i].draw();
    }
    StdDraw.show();
    StdDraw.pause(20);
    if (t < limit) {
        pq.insert(new Event(t + 1.0 / refresh, null, null));
    }
}

Nothing fancy going into this function. We just redraw every particle after clearing previously drawn sets of particles.

public void simulate(double limit) {
    StdDraw.setCanvasSize(800, 800);
    pq = new MinPQ<Event>();
    for (int i = 0; i < particles.length; i++) predict(particles[i], limit);
    pq.insert(new Event(0, null, null));

    while (!pq.isEmpty()) {
        Event event = pq.delMin();
        if (!event.isValid()) continue;
        Particle a = event.getA();
        Particle b = event.getB();

        for (int i = 0; i < particles.length; i++)
            particles[i].move(event.getTime() - t);
        t = event.getTime();

        if (a != null && b != null) a.bounceOff(b);
        else if (a != null && b == null) a.bounceOffVerticalWall();
        else if (a == null && b != null) b.bounceOffHorizontalWall();
        else if (a == null && b == null) redraw(limit);

        predict(a, limit);
        predict(b, limit);
    }
}

Previously mentioned steps can be seen here in this simulate function. Initially, we predict straight line trajectory of every particle. We insert an event with 0,null ,null just to trigger the starting of the simulation. After that we delete minimum item in the priority queue , check if they are valid or not.

After we get a valid event we move every particle forward and check if any collision have occurred or not. Then , we check if both particles are present. If both are present , we call bounceOff function in order to mimic the collision which eventually updates the velocity of the particles. And if either of these two particles are null then they are bounced off x or y axes respectively. Finally, we predict the new straight line trajectory for both particles.

At the end, we have a complete Molecular Dynamics Simulation of Hard Spheres.

There are many more articles if you wanna get started into Machine Learning , or Build Your Own AI Powered game, or maybe overclock your NVIDIA GPU fan with simple GUI